中学数学　図形が難しい子への教え方　2022年1月公開記事

図形が苦手な子の中で「特徴がわからない子」に対しては

大体この2つです。

1 たくさん図形を見て見分ける
例がたくさんあればあるほど、対象の共通項を取り込むことができて、特徴がわかるようになります。

たくさんの二等辺三角形を見れば、二等辺三角形の特徴がなんとなくわかります。

そこで、

→特徴を言葉に変換

→変換した言葉をさらに式に変換

ここまでやると、証明問題が書けるようになります。

読んで理解したことを式にする。

日本語を数学語に翻訳する必要があるからです。

2 具体物を作って、触ってみる

これは小学生でもやります。

展開図がわからないと

• 表面積
• 側面積

などの問題が難しくなります。

「円錐を作ってごらん」

とやると、すごく試行錯誤します。

まずは、できたものをバラすところから。

ばらばらにすると、どうやって構成されているか要素を出すことができます。

また、向きによって長さや角度が違って見える子もいます。

（そういう子に限って自分の感覚で見えた長さや角度を信じる傾向にある。なんでそんなに自分を信じられるのか。

もしかしたら、他に信じるものがないから信じざるを得ないのかもしれない。）

なので、具体物を作り、触ってもらいます。

円と円周角の関係は割とつまづきどころ。

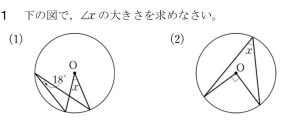
（2）はできるのに、（1）はわからない、という子が非常に多いです。

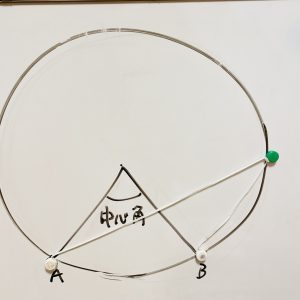
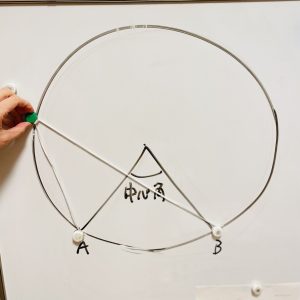
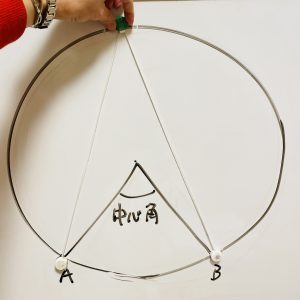
磁石とゴムで実際に動かして、同一の弧の円周角はどこでも角度が等しいことを見て動かしてもらいます。

少し、時間はかかるけど

1 たくさん図形を見て見分ける

2 具体物を作って、触ってみる

この2つです。

すごく普通のことですが、全然違います。