算数が楽しくなる本　2017年6月公開記事

算数好きですか？

何人もの生徒を教えていて「わかる」への道筋が、子どもによって２種類に別れるな、と思います。

①理屈がわかると進めるタイプ

このタイプはとにかく「どうしてそうなっているか」がわからないとすすめない。

なので、「え？そんなところで？」というようなところでつまづいていることがあるので、

わかりやすく仕組みを理解できるように説明するのが大事です。

②パターンをある程度習得させると理屈がわかるタイプ

こちらのタイプは理屈は後回し。

ひとまず、パターンを身体に覚えさせて、後から仕組みを説明するようにすると、なるほどとなるタイプ。

先に仕組みや理屈を教えると、混乱してわけがわからなくなりがちです。

身体に覚えさせていくのが大事。

私達大人も、掛け算の仕組みって実は理解してませんよね。

２×５と５×２って実は違うんですよ。

２×５は２＋２＋２＋２＋２という意味。

５×２は５＋５という意味。

だから、小学校では

だと、式は２×５＝10となり、５×２＝10ではやり直しになることがあるんですね。

でも、そんな説明ができる親がどのくらいいるでしょうか??

中学では乗法の交換法則によって２×５も５×２も同じものとして扱われます。

その辺がひたすら具体物のみを扱う算数とは違うところです。

で、 ①と②、どちらの種類の子どもさんだったとしても、生活の中で数字や数、長さや重さに触れておくのはとても大切です。

なぜなら、中学までの算数・数学はイメージがとても大切だからです。

円柱の体積だったら輪切りのきゅうりが◯センチ重なっているイメージ。

速さや水溶液といった単位あたりの量を考えるときも、

道を同じ速さで進むイメージや、水に食塩を溶かすイメージができて絵がかければときやすくなります。

そういうのは、日々の生活の中で少しずつ取り入れることができます。

例えば小さい子なら、

• いちごやプチトマト、ぶどうなどを家族の人数分のお皿を出して均等にわけさせたり、
• レゴを組み立てるときにポチの数を２✕２で４ポチと表現したり、
• お風呂のタイルを数えてみたり

そんなちょっとしたところに算数を入れてみると、子どもは学校でならった時に

「あ、なんか知ってる」と思えるのです。

しっかり読むわけではないですが、こんな本もいいですね。

「学研　算数図鑑」

（クリックでAmazonにとびます）

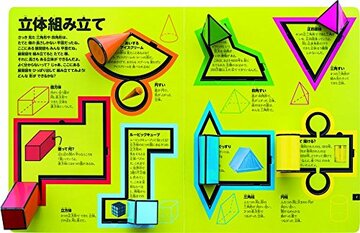
この本のいいところは、立体図形が本のまま作れるところです。

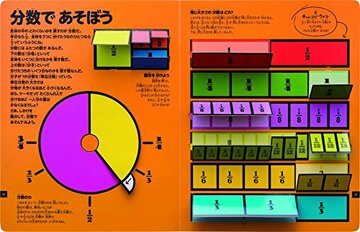
分数はこんな感じ。

しかけ絵本みたいで楽しいです。

わかってなくてもいいんです。

まずは、身近に感じるところから。

今日も読んでいただきありがとうございます。